Table of Contents

1. research
   1. the complete regular map
   2. a strikingly motivating example
   3. questions to ponder at
   4. literature
   5. results
   6. bibliography
2. presenting
3. jmm
   1. talks
   2. art
   3. balloons
4. seattle
1. am
2. pm
5. acknowledgements

---

i. research

The motivation to study pure topological maps arises from simple polyhedra. In a sense, any polyhedron may be realised as an embedding of a graph into a topological surface — one that splits the surface into a disjoint union of topological discs.

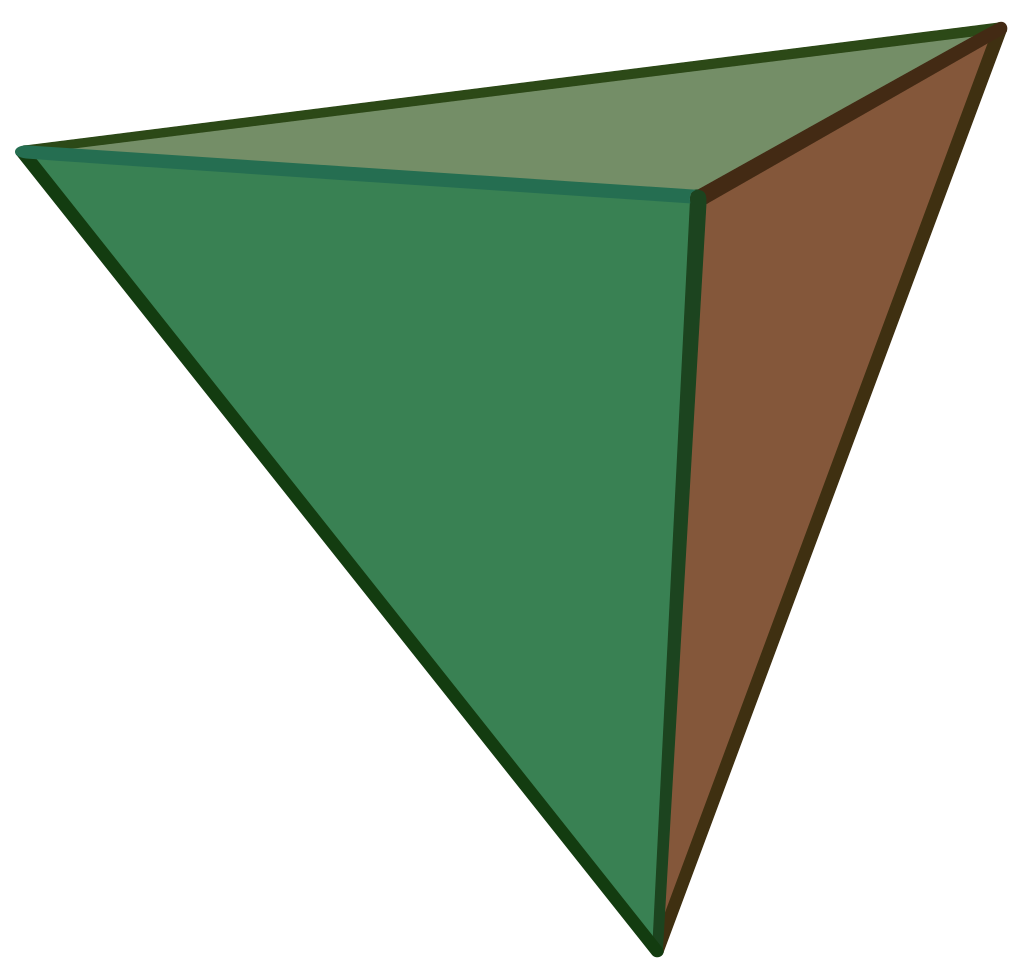
i.i the complete regular map

In our project, we study maps which are

• regular, in the sense that they exhibit maximal symmetry;
• complete, in the sense that the underlying graph is complete.

Precisely, the regularity condition is satisfied if and only if the complete regular map \(M: K_n \hookrightarrow \Sigma_g\) exhibits \(n \cdot(n-1)\) rotational symmetries. To state an example, one may easily verify that the tetrahedron \(K_4 \hookrightarrow \Sigma_1\) has \(4 \cdot 3\) symmetries.

An object classically defined in a purely combinatorial sense, we are interested in a construction of complete regular maps that utilises the power of number theory. Why, you might ask?

i.ii a strikingly motivating example

In the complex plane, we are working with the lattice \(\mathbb Z[i]/(1+2i)\), which is (isomorphic to) the field of five elements \(\mathbb F_5\). These elements are the vertices of \(K_5\).

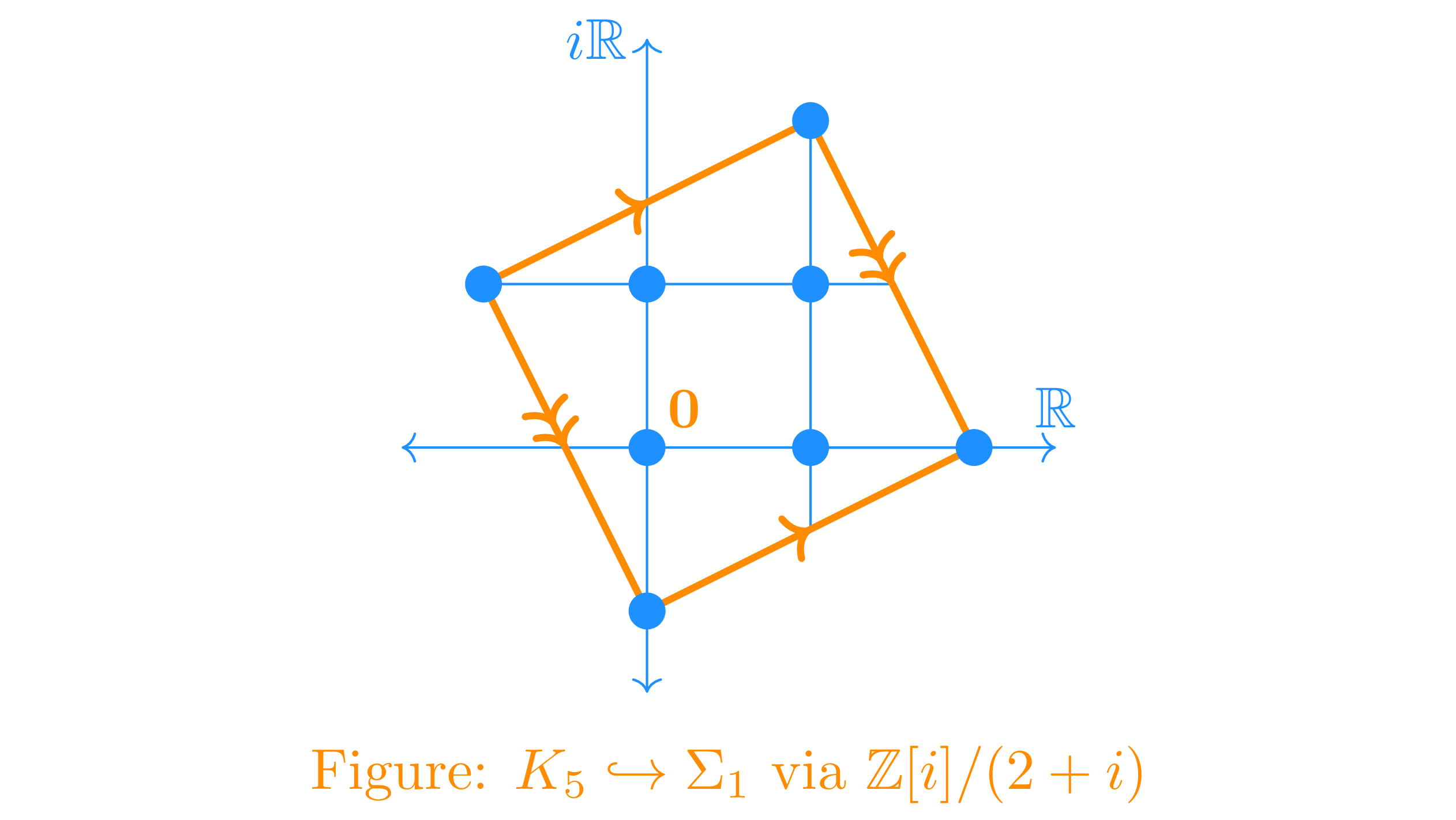
Can you spot all equivalence classes \(\text{mod } (1+2i)\)?

\(\textit{Hint.}\) Follow the arrows. Where do the vertices eventually land?

It is not too difficult to check that what we have is a topological map. As for the completeness condition, each vertex is connected via exactly one edge!\(^{(*)}\) Finally, the regularity condition is satisfied once we look at

\[\begin{equation*} z \mapsto i^k z + x \quad \text{ for } \quad x \in \mathbb Z[i], \quad k = 0,1,2,3. \end{equation*}\]

Starting at some vertex \(z\), there are five translations (counting each vertex) and four different rotations \(i^k\) in the complex plane; yielding an intended \(5 \cdot 4\) symmetries for the five-vertex map.

(*) Pick an edge, and try to think of how it would extend to connect with an appropriate edge upon assembling the torus.

i.iii questions to ponder at

1. \((2+i)\) is a prime ideal of norm \(5\). The resulting map has \(5\) vertices.

   Would other prime ideals of the same norm induce complete regular maps? How about prime ideals of the same norm e.g \((1+2i), (2-i)\)? Would they produce new maps on 5 vertices?

2. \(\mathbb Z[i]\) is the \(4^{th}\) cyclotomic ring. In words, \(i\) is the fourth root of unity, \(i^4 = 1\).

   Is there a relation between the \(n^{th}\) root of unity and the map on \(n+1\) vertices? How might the geometry of the lattice \(\mathbb Z[x]/\mathfrak p\) change, for some prime ideal \(\mathfrak p\)?

3. This is an algebraic construction of the complete regular map on \(n=5\) vertices.

   Can we construct more, perhaps all complete regular maps by the same method?

i.iv literature

Here, we attempt to give an argument for why it might be reasonable to pursue the third question.

\(\textbf{Theorem}\text{ [Biggs (1971)].} \textit{ Cayley maps associated to finite fields } \mathbb F_n \textit{ on } n=p^f \textit{ elements }\) \(\textit { give rise to complete regular maps on } n \textit{ vertices. }\)

\(\textbf{Theorem}\text{ [James & Jones (1985)].} \textit{ Biggs' construction gives rise to all complete regular }\) \(\textit{maps. }\)

A simple yet important consequence of these two results is the following:

\(\textbf{Corollary.} \textit{ A complete regular map has } n = p^f \textit{ vertices }.\)

With this, we may strategize our focus on constructing a complete regular map on \(n = p^f\) vertices, for odd \(p\). Next, let me draw your attention to the following two theorems.

\(\textbf{Theorem}\text{ [James & Jones].} \textit{ Let } p \textit{ be an odd prime. Then, there are } \phi(n-1)/f \textit{ isomorphism }\) \(\textit{ classes of complete regular maps on } n=p^f \textit{ vertices.}\)

\(\textbf{Theorem}\text{} \textit{ Let } p \textit{ be an odd prime. Then, there are } \phi(n-1)/f \textit{ distinct prime ideals in } \mathbb Z[\zeta_{n-1}]\) \(\textit{ of norm } p.\)

\(\phi(n-1)/f\) prime ideals, \(\phi(n-1)/f\) complete regular maps… surely, an attempt to study a possible link between the two objects cannot be too hopeful.

i.v results

Not too hopeful indeed, we constructed all complete regular maps on \(n=p^f\) vertices for odd \(p\). This is the very-first milestone in our reseach. Then follows a classification of complete regular maps via prime ideals. This starts with the following theorem,

\(\textbf{Theorem.} \textit{ For odd } p \textit{, every distinct prime ideal } \mathfrak p \subset \mathbb Z[\zeta_{n-1}] \textit{ of index } p \textit{ induces a complete }\) \(\textit{regular map } M_\mathfrak p \textit{ on } n=p^f \textit{ vertices.}\)

In words — given a prime ideal \(\mathfrak p,\) a complete regular map \(M_\mathfrak p\) is supplied. Naturally comes the following question,

\(\textbf{Proposition.} \textit{ Distinct } \mathfrak p \textit{ give rise to distinct } M_\mathfrak p.\)

to which we have a positive answer! For us, this means one thing for sure,

\(\textbf{Corollary.} \textit{ For odd } p \textit{, there exists a bijection between prime ideals } \mathfrak p \subset \mathbb Z[\zeta_{n-1}] \textit{ of norm } p\) \(\textit{ and isomorphism classes of complete regular maps on } n=p^f\textit{ vertices}.\)

This is credited to the fact that there exist \(\phi(n-1)/f\) prime ideals, each of which induce a distinct complete regular map. But, there are at most \(\phi(n-1)/f\) complete regular maps.

To mention another research direction, we studied the resulting action of the Galois group on the set of complete regular maps upon permuting the set of prime ideals. This is well-explained in the final segment of the talk, which I attach below.

i.vi bibliography

• Norman Biggs. Automorphisms of imbedded graphs. Journal of Combinatorial Theory, Series B, 11(2):132–138, 1971.
• Norman L. Biggs and A. T. White. Permutation Groups and Combinatorial Structures. Cambridge University Press, 1979.

---

ii. presenting

On January 8th, we presented our talk in the American Mathematical Society’s special session on Polymath Jr research.

to the abstract

to the talk

---

iii. jmm

50+ concurrent talks, 9 hours a day, for 4 consecutive days. Overwhelming — ly positive, I would say?

iii.i talks

I am almost never a take-a-picture-of-the-slides type of guy, but…

iii.ii art

iii.iii balloons

bonus: mathematically bent theatre

Some really cool math sketches!

---

iv. seattle

exploring the city.

iv. am

a really beautiful city at day…

iv.ii pm

… even more so at night.

---

v. acknowledgements

I am indebted to Adjmain Yamin, Connor Stewart, and Professor Lisa Berger for their valuable mentoring. To my collaborators, Jimmy Zhang and Matthew Snodgrass, I am beyond humbled to have worked with two such outstanding individuals. May I additionally acknowlege the Polymath Jr, the Deans of Constructor University, and Professor Sören Petrat, without whom this opportunity would not have been possible.

Finally, I would like to acknowledge my friends and family, without whom I would not stand till this day.

Now, is it Friday already? I am still jet-lagging…

\(\boxed \xi\)