mathPix to moodle.sty
a RegEx project to speed up digital transformation to moodle
Table of Contents
i. a minimal working example
Here, we have an SAT mathematics exercise.
With 200+ students in my class, it is very difficult to give personalized feedback. Therefore, we would like to have this exercise in nice digital format.
This may of course be done using moodle.sty, and lots of copy-pasting if you’d like. It can, however, become impractical to repeat that for 1000+ questions. We propose the following question: is there a better way?
Yes is the answer to the previous question. Instead of mindlessly copy-pasting questions, we decided to invest time and effort into a tool that does most of the work for us.
-
moodleis an open-source LMS software utilised by many institutions worldwide, including mine. -
mathPIXis an OCR software that specializes in rendering \(\LaTeX\). -
moodle.styis a \(\LaTeX\) package that mass-imports questions withmathcontent intomoodle.
The goal of this project is to start with pdf documents rendered into text using mathPIX, and then utilise regEx to bring it to a moodle.sty-compatible format for import into moodle.
This notebook mathPix-to-moodle.sty aims to achieve our stated goal for one question. Then, the notebook massPix-to-moodle.sty generalises the construction for masses of questions. If you would like to immediately jump to there, please use
> massPix-to-moodle.sty
Let us now examine the mathPIX text input.
ii. processing
import re
We start by reading extracted text from our file.
def read_text_file(file_path):
with open(file_path, 'r', encoding='utf-8') as file:
content = file.read()
return content
I have included three minimal working examples in the mwe directory.
-
q-multi.txtis a multiple-choice question; -
q-shortanswer.txtis a short-answer question; -
q-shortanswer-media.txtis a short-answer question with media.
The input is not too nice, but we may start working with it for now. Below you will see the formatted output of the very-same question we saw above.
N.B: this was done using mathPIX, the \(\LaTeX\) OCR software.
txt = read_text_file("mwe/q-shortanswer-media.txt")
print(txt)
\section*{Question Difficulty: Hard}
\section*{Question ID 09d21d79}
\begin{tabular}{|l|l|l|l|l|}
\hline Assessment & Test & Domain & Skill \\
SAT & Math & Advanced Math & Nonlinear functions & Difficulty \\
$\square \square$ \\
\hline
\end{tabular}
\section*{ID: 09d21d79}
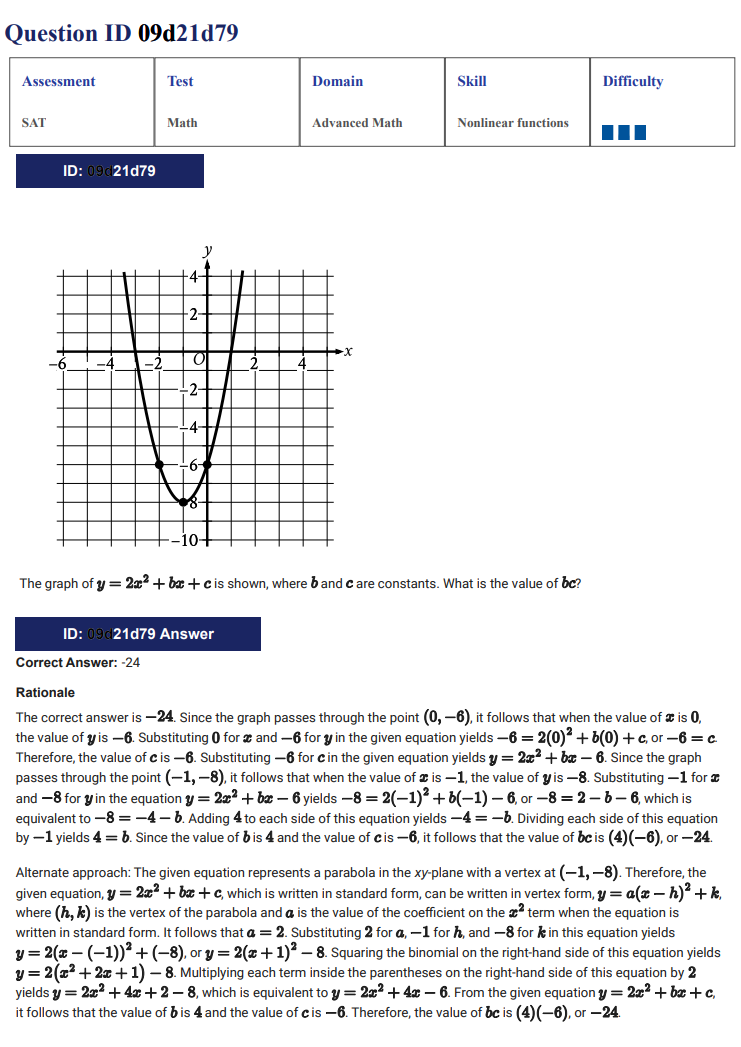
The graph of $y=2 x^{2}+b x+c$ is shown, where $b$ and $c$ are constants. What is the value of $b c$ ?
\section*{ID: 09d21d79 Answer}
Correct Answer: -24
\section*{Rationale}
The correct answer is -24 . Since the graph passes through the point $0,-6$, it follows that when the value of $x$ is 0 , the value of $y$ is -6 . Substituting 0 for $x$ and -6 for $y$ in the given equation yields $-6=20^{2}+b 0+c$, or $-6=c$. Therefore, the value of $c$ is -6 . Substituting -6 for $c$ in the given equation yields $y=2 x^{2}+b x-6$. Since the graph passes through the point $-1,-8$, it follows that when the value of $x$ is -1 , the value of $y$ is -8 . Substituting -1 for $x$ and -8 for $y$ in the equation $y=2 x^{2}+b x-6$ yields $-8=2-1^{2}+b-1-6$, or $-8=2-b-6$, which is equivalent to $-8=-4-b$. Adding 4 to each side of this equation yields $-4=-b$. Dividing each side of this equation by -1 yields $4=b$. Since the value of $b$ is 4 and the value of $c$ is -6 , it follows that the value of $b c$ is $4-6$, or -24 .
Alternate approach: The given equation represents a parabola in the $x y$-plane with a vertex at $-1,-8$. Therefore, the given equation, $y=2 x^{2}+b x+c$, which is written in standard form, can be written in vertex form, $y=a x-h^{2}+k$, where $h, k$ is the vertex of the parabola and $a$ is the value of the coefficient on the $x^{2}$ term when the equation is written in standard form. It follows that $a=2$. Substituting 2 for $a,-1$ for $h$, and -8 for $k$ in this equation yields $y=2 x--1^{2}+-8$, or $y=2 x+1^{2}$ - 8 . Squaring the binomial on the right-hand side of this equation yields $y=2 x^{2}+2 x+1-8$. Multiplying each term inside the parentheses on the right-hand side of this equation by 2 yields $y=2 x^{2}+4 x+2-8$, which is equivalent to $y=2 x^{2}+4 x-6$. From the given equation $y=2 x^{2}+b x+c$, it follows that the value of $b$ is 4 and the value of $c$ is -6 .
Therefore, the value of $b c$ is $4-6$, or -24 .
Question Difficulty: Hard
ii.i no rationale
We remove rationale for the sake of simplicity. In a practical sense, students may still retain the rationale section of a question by looking up the question id, which in this case is 09d21d79. One may additionally refer to CollegeBoard, choose the respective topic and difficulty, then look up the code using ctrl + f.
It is merely a matter of taste. To proceed, notice that rationale is marked by starting with \section*{Rationale} and proceeding until the start of the following question.
def remove_rationale(text):
# This pattern looks for '\section*{Rationale}' and removes everything until the next '\section*{' or end of string
text = re.sub(r'\\section\*\{Rationale\}.*?(?=\\section\*|\Z)', '', text, flags=re.DOTALL)
return text
txt = remove_rationale(txt)
print(txt)
\section*{Question Difficulty: Hard}
\section*{Question ID 09d21d79}
\begin{tabular}{|l|l|l|l|l|}
\hline Assessment & Test & Domain & Skill \\
SAT & Math & Advanced Math & Nonlinear functions & Difficulty \\
$\square \square$ \\
\hline
\end{tabular}
\section*{ID: 09d21d79}

The graph of $y=2 x^{2}+b x+c$ is shown, where $b$ and $c$ are constants. What is the value of $b c$ ?
\section*{ID: 09d21d79 Answer}
Correct Answer: -24
iii. data extraction
We outline the extraction process of four key elements: <ans>, <id>, <body>, <type>.
iii.i correct answer
Next, let us fetch the correct answer <ans>. This is always found within the string Correct Answer: <ans>. This is an easy observation once you inspect the pdf documents containing the exercises.
def fetch_correct_answer(text):
# Find the correct answer, allowing for negative signs in the answer
match = re.search(r'Correct Answer:\s*(-?\d+)', text)
return match.group(1) if match else None
ans = fetch_correct_answer(txt)
print(ans)
-24
iii.ii question id
To fetch <id>, we look up the string \section*{Question ID <id>}.
def fetch_question_id(text):
# Find the question ID
match = re.search(r'\\section\*\{\s*Question ID\s+(\w+)\s*\}', text)
return match.group(1) if match else None
q_id = fetch_question_id(txt)
print(q_id)
09d21d79
iii.iii question body
The question body is always in the form
\section*{ID: <id>}
<body>
<choices> %if any
\section*{ID: <id> Answer}
def fetch_question_body(text, question_id):
# Pattern to capture everything between \section*{ID: <question-id>} and the start of choices (A., B., C., or D.)
pattern = rf'\\section\*\{{ID: {question_id}\}}\s*(.*?)(?=\s*[A-D]\.\s|\s*\\section\*\{{ID: {question_id} Answer\}})'
match = re.search(pattern, text, flags=re.DOTALL)
if match:
return match.group(1).strip()
return None
q_body = fetch_question_body(txt, q_id)
print(q_body)
ID: 09d21d79
iii.iv shortanswer or multi?
To determine question type, we inspect <ans>.
-
If
<ans>is a literalA - D, then clearly this is amultiquestion. -
Otherwise, there is a numerical or fractional answer of the form
a.bcord/ewhich characterizes ashortanswerquestion.
def determine_question_type(answer):
# Determine if the question is a short answer or multiple-choice based on the answer format
if re.match(r'^-?\d+$|^-?\d+/\d+$', answer): # Checks if answer is a number (including negative) or fraction
return "shortanswer"
elif re.match(r'^[A-D]$', answer): # Checks if answer is A, B, C, or D
return "multi"
return None
q_type = determine_question_type(ans)
print(q_type)
shortanswer
iv. parsing
Upon constructing the necessary multi and shortanswer templates, we combine our elements in a parse_question function to give the intended result.
iv.i question templates
iv.i.i - shortanswer
The shortanswer moodle template is given as follows,
\begin{shortanswer}[fraction=100]{<id>}
<body>
\item[fraction=100] <ans>
\end{shortanswer}
def format_shortanswer(question_id, question_body, answer):
# Format short answer question
formatted = f"""\\begin[fraction=100]}
{question_body}
\\item[fraction=100] {answer}
\\end"""
return formatted
#q = format_shortanswer(q_id, q_body, ans)
#print(q)
This finishes the job for shortanswer-type questions. Now remains to handle the multi case, specifically with choices.
iv.i.ii - multi
def extract_choices(text):
# Extract choices while handling multiline content after each label (A., B., C., D.)
choices = []
pattern = r'([A-D]\.\s.*?)(?=\s*[A-D]\.|\\section\*\{ID:|$)' # Match choices A., B., C., D.
matches = re.findall(pattern, text, flags=re.DOTALL)
for match in matches:
# Normalize line breaks and strip leading/trailing whitespace
choices.append(match.replace('\n', ' ').strip())
# Remove the choice labels (A., B., C., D.) from each extracted choice
choices = [choice[2:].strip() for choice in choices] # Removes label (e.g., "A. " to keep just the choice)
return choices if choices else None
q_choices = extract_choices(txt)
print(q_choices) ## returns none, as the question is short-answer.
None
def format_multi(question_id, question_body, answer, choices):
# Map answer to corresponding choice and format multiple-choice question
if len(answer) == 1:
answer_index = ord(answer) - ord('A')
items = [f"\\item * {choice}" if i == answer_index else f"\\item {choice}" for i, choice in enumerate(choices)]
formatted_items = "\n".join(items)
formatted = f"""\\begin}
{question_body}
{formatted_items}
\\end"""
else:
formatted = "None"
return formatted
q = format_multi(q_id, q_body, ans, q_choices)
print(q) ## returns none, as the question is short-answer.
None
iv.ii altogether
# Main function to orchestrate parsing and formatting
def parse_question(text):
text = remove_rationale(text)
question_id = fetch_question_id(text)
answer = fetch_correct_answer(text)
question_body = fetch_question_body(text, question_id)
if not all([question_id, answer, question_body]):
return "Error: Unable to parse question properly."
question_type = determine_question_type(answer)
if question_type == "shortanswer":
return format_shortanswer(question_id, question_body, answer)
elif question_type == "multi":
choices = extract_choices(text)
if choices and len(choices) == 4:
return format_multi(question_id, question_body, answer, choices)
else:
return "Error: Multiple-choice question lacks choices or has an incorrect format."
else:
return "Error: Unknown question type or unrecognized answer format."
Here is your parsed question…
iv.ii.i output
q = parse_question(txt)
print(q)
\begin{shortanswer}[fraction=100]{09d21d79}

The graph of $y=2 x^{2}+b x+c$ is shown, where $b$ and $c$ are constants. What is the value of $b c$ ?
\item[fraction=100] -24
\end{shortanswer}
Looking good.
iv.ii.ii brief note
Before we proceed, one must note that

is premature, in the sense that \(\LaTeX\) may only process the media file within this link once it is
- downloaded;
- properly referenced within a directory.
In the massPix-to-moodle.sty notebook, there is a media() function that precisely takes care of this matter.